[5강] 통계적 지표(왜도와 첨도)

왜도(Skewness)

[4강] 데이터의 산포도 측정(분산, 표준편차, 범위 등)에서 살펴본 분산과 같은 측정방법은 한계가 있다. 먼저, 데이터가 대칭적인지를 알 수 없다. 평균을 기준으로 큰 값이 많은지 작은 값이 많은지 아니면 값들이 균등하게 분포되었는지 알 수가 없다. 이것을 측정하는 것이 왜도이다.

왜도의 계산은 데이터 각 값과 평균의 차이를 세제곱 한 값을 평균하면 된다. 여기에 표준편차 한 단위 당 값을 구하기 위해서 표준편차를 세제곱해서 나눠준다. 데이터 각 값과 평균의 차이를 세제곱함으로써 평균으로부터 멀리 있는 값에 가중치를 준다고 생각하면 된다. 그리고 세제곱을 해 주므로 +, - 기호를 통해서 평균을 기준으로 큰 값인지 작은 값인지 구분해 줄 수 있다.

양의 왜도 값을 가지면, 오른쪽 꼬리가 길다고도 한다. 평균보다 큰 극단적인 값들이 세제곱되어세제곱 되어 큰 가중치를 갖고, 평균보다 작은 값들은 평균과 큰 차이가 안 난다면, 데이터는 양의 왜도를 가지게 된다. 반대로 음의 왜도 값을 가지면 왼쪽 꼬리가 길다고도 한다. 평균보다 작은 극단적인 값들이 세제곱 되어 큰 가중치를 갖고, 평균보다 큰 값들이 평균에 가까이 있다면, 데이터는 음의 왜도를 가지게 된다.

다음과 같은 두 개의 데이터가 있다고 하자. list a 는 7,5,10이라는 극단적인 값이 있고, 평균과 가까운 작은 값들에 값이 몰려있다. list b는 평균과 가까운 큰 값들에 값이 몰려있고, 평균보다 작은 0.1, 0.65 같은 극단적인 값을 갖고 있다. 

A = [0.1,0.65,1.3,1.75,2.6,3.8,4.0,4.7,5,10]
B = [0.1,0.65,5.0,6.2,6.5,6.9,7.7,8.5,9,10]

위의 분포로 그래프를 그리면 아래 그림 1과 같은 그래프를 얻을 수 있다. 그림 1을 보면 A 분포로 만든 빨간색 선은 오른쪽 꼬리가 길게 생긴 것을, B분포로 만든 파란색 선은 왼쪽 꼬리가 길게 생긴 것을 확인할 수 있다.(그래프를 만들 때 lonormal 분포 같은 개념 등이 들어가서 복잡해지니까 그래프 만드는 과정은 생략한다.)

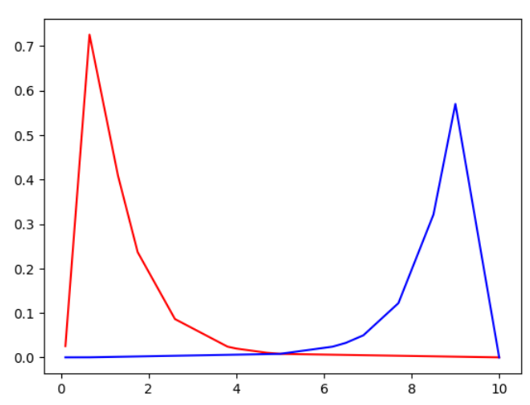
그림1: 양의 왜도 그래프와 음의 왜도 그래프 비교

왜도값은 위에서 말한 계산식을 그대로 적용하면 쉽게 구할 수 있다. 먼저, 분포 b 의 평균(mu_b)을 먼저 구하고, 표준편차(std_b)를 구한다. 다음으로 분포 b의 각 항목값에서 평균을 빼주고 세제곱 한 값의 합을 데이터 수로 나누어준다. 마지막으로 표준편차의 세제곱을 나누어서 표준편차 한 단위 당 값을 구해주면 된다. scipy의 stats 모듈의 skew 함수를 사용하면 이 과정을 생략하고 쉽게 왜도를 구할 수 있다.

# numpy, scipy 라이브러리 참조
import numpy as np
import scipy.stats as stats

# 데이터 설정
b = [0.1,0.65,1.3,1.75,2.6,3.8,4.0,4.7,5,10]
mu_b = np.mean(b)
std_b = np.std(b)
skew_b = (sum([(i - mu_b)**3 for i in b])/std_b**3)/len(b)
# 직접 계산한 왜도값(skew_b)과 scipy를 통해 구한 왜도값(stats.skew(b)) 비교
print(stats.skew(b), skew_b)

 

첨도(Kurtosis)

분산과 같은 측정방법의 또다른 한계는 극단적인 값(꼬리 부분)이 얼마나 많이 발생하는지 알기 어렵다는 점이다. 데이터 분포에서 극단적인 값이 얼마나 있는지와 중심부 데이터가 얼마나 많은지 측정하는 것도 중요한데, 이것을 측정하는 것이 첨도이다.

첨도의 계산은 데이터 각 값과 평균의 차이를 네제곱한 값을 평균하면 된다. 여기에 표준편차 한 단위 당 값을 구하기 위해서 표준편차를 네 제곱해서 나눠준다. 데이터 각 값과 평균의 차이를 네제곱함으로써 평균으로부터 멀리 있는 꼬리값에 가중치를 준다고 생각하면 된다. 이때 평균 근처에 데이터가 몰려있고 일부의 극단적인 값이 있는 경우 표준편차가 작아져서 분모가 작아지고, 극단적인 일부 값들과 평균의 차이가 네제곱되면서 분자가 커지는 효과가 더해져 첨도가 커진다. 반대로 데이터가 고르게 퍼져있는 경우 표준편차가 커지면서 분모가 증가하고, 네제곱이 되면서 분자를 크게 하는 극단적인 값들이 줄어들면서 첨도가 작아진다. 

다음과 같은 두 개의 데이터가 있다고 하자. list C 는 2부터 10까지 차례대로 증가하는 데이터인 반면, list D는 평균에 대부분의 값이 몰려있는 동시에 일부 극단적인 값인 2, 10이 있다. 

C = [2,3,4,5,6,7,8,9,10,10]
D = [2,6,6,6,6,6,6,7,7,10]

위의 분포로 그래프를 그리면 아래 그림 2와 같은 그래프를 얻을 수 있다. 중앙에 데이터가 많지만 극단값이 발생하는 D 데이터의 만든 파란색 그래프가 더 뾰족한 것을 확인할 수 있다.

그림2: 첨도에 따른 그래프 모양

첨도값은 위에서 말한 계산식을 그대로 적용하면 쉽게 구할 수 있다. 먼저, 분포 d의 평균(mu_d)을 먼저 구하고, 표준편차(std_d)를 구한다. 다음으로 분포 d의 각 항목값에서 평균을 빼주고 네제곱 한 값의 합을 데이터 수로 나누어준다. 마지막으로 표준편차의 네제곱을 나누어서 표준편차 한 단위 당 값을 구해주면 된다. 데이터의 첨도는 정규분포의 첨도인 3과 비교할 때 의미가 있기 때문에(표준편차보다 얼마나 뾰족한지를 확인) 3을 차감해 주면 데이터가 얼마나 뾰족한지를 나타내는 최종적인 값이 나온다. scipy의 stats 모듈의 kurtosis 함수를 사용하면 이 과정을 생략하고 쉽게 첨도를 구할 수 있다.

# numpy, scipy 라이브러리 참조
import numpy as np
import scipy.stats as stats

# 데이터 설정
d = [2,3,4,5,6,7,8,9,10,10]
mu_d = np.mean(d)
std_d = np.std(d)
kurto_d = (sum([(i - mu_d)**4 for i in d])/std_d**4)/len(d) - 3
# 직접 계산한 첨도값(kurto_d)과 scipy를 통해 구한 첨도값(stats.kurto(d)) 비교
print(stats.kurtosis(d), kurto_d)

주식 수익률 데이터의 왜도와 첨도 분석

yahoo finance 라이브러리를 통해서 애플과 엔비디아의 일일 수익률 데이터 분포를 분석해보자. 기간은 2024-01-01 ~ 2024-11-30으로 잡고 download 함수를 사용해서 data를 종가 데이터를 받아온다. 받아온 데이터에서 "Adj Close" 컬럼을 선택해서 애플과 엔비디아의 price 데이터를 만든다. pct_change 함수를 통해서 조정종가의(Adj close) 일일 수익률을 구해서 각 종목의 returns 데이터를 만든다. scipy 라이브러리를 통해서 각 종목의 왜도와 첨도를 구하고, 데이터프레임으로 정리를 하면 수익률 데이터의 왜도와 첨도를 분석할 준비가 끝난다.

# 참조 라이브러리 설정
import numpy as np
import pandas as pd
import yfinance as yf
import scipy.stats as stats

# 데이터 입수 시작일과 종료일 설정
start = '2024-01-01'
end = '2024-11-30'
# 데이터 다운로드
data = yf.download(["AAPL", "NVDA"], start=start, end=end)
# 데이터에서 종목별로 조정종가("Adj Close")를 구한 뒤 일일 수익률 데이터로 변환
price_aapl = data["Adj Close"]["AAPL"]
returns_aapl = price_aapl.pct_change()[1:]
price_nvda = data["Adj Close"]["NVDA"]
returns_nvda = price_nvda.pct_change()[1:]
# 일일 수익률 데이터를 이용한 종목별 왜도와 첨도의 산출
skew_aapl = stats.skew(returns_aapl)
skew_nvda = stats.skew(returns_nvda)
kurt_aapl = stats.kurtosis(returns_aapl)
kurt_nvda = stats.kurtosis(returns_nvda)
# 산출한 값을 딕셔너리 데이터 형식으로 정리
raw = {"stocks":["애플", "엔비디아"],
       "skewness":[float(skew_aapl), float(skew_nvda)],
       "kurtosis":[float(kurt_aapl), float(kurt_nvda)]}
# 데이터프레임으로 만들어서 출력
df = pd.DataFrame(raw)
print(df.to_string(index=False))

작성한 코드를 출력하면 아래 그림 3과 같은 결과를 얻을 수 있다. 

그림3: 애플과 앤비디아의 왜도와 첨도 산출 결과

결과를 보면 애플의 왜도가(+) 앤비디아보다 더 크고 첨도도 더 크다는 것을 파악할 수 있다. 애플의 왜도와 첨도가 더 크다는 것은 애플의 일일수익률 분포가 꼬리가 더 두껍고 극단적인 값이 더 많이 발생한다는 것을 의미한다. 2024년도에는 일일수익률만 놓고 보면 정규분포보다 큰 수익률의 변동은 엔비디아보다 애플 주식에서 더 많이 발생했다.