[7강] 연속형 확률변수

연속형 확률변수

확률변수란 결괏값이 확률적으로 정해지는 변수이다. 결괏값이란 주사위의 숫자처럼 실제로 나온 값일 수도 있고, 동전 던지기에서 앞면을 1, 뒷면을 0으로 가정하는 것처럼 임의로 부여한 값일 수도 있다. 확률변수들을 하나씩 셀 수 있는지에 따라서 이산형 확률변수, 연속형 확률변수로 구분한다.

연속형 확률변수는 결괏값이 무한히 많고 연속적인 값을 가질 수 있는 확률변수이다. 결과가 무한히 많으므로 특정한 값 하나가 나올 확률은 0으로 의미가 없고, 항상 구간에 걸쳐서 확률을 계산한다. 따라서 특정 구간에 대해서 확률을 계산하는 확률밀도함수(PDF)를 사용한다. 

식1: 확률밀도함수(PDF)

확률밀도함수(PDF: Probability Density Function)는 아래 그림 1에서 확인할 수 있는 것처럼 모든 함숫값이 0보다 같거나 크고, 전체 확률은 1이라는 성질을 가진다.

그림1: 확률밀도함수(PDF) 성질

균등 분포(Uniform Distribution)

균등분포는 연속형 확률변수의 틀에서도 정의될 수 있으며, 일정한 구간 내에서 모든 값에 대해 동일한 확률밀도를 갖기 때문에 그 확률밀도함수(PDF)를 아래와 같이 정의할 수 있다.

그림2: 연속형 확률변수의 균등분포에서 확률밀도함수 정의

위 그림 2에서 정의된 확률밀도함수(PDF)의 아래쪽 면적은 누적분포함수(CDF)가 되고, 이는 확률밀도함수(PDF)의 적분값이다. 누적분포 함수는 x = a 일 때 0이었다가 x 값이 커지면서 점점 증가하다가 x 가 b값이 되면 1이 되는 구조이다.

식2: 연속형 확률변수의 균등분포에서 누적분포함수

균등분포의 확률밀도함수는 numpy의 linspace 함수를 통해서 쉽게 구현할 수 있고, 누적분포함수는 위 식 2를 이용해서 구현할 수 있다. 

import numpy as np
import matplotlib.pyplot as plt

# 확률밀도함수 구현
a = 0.0
b = 8.0
x = np.linspace(a, b, 100)
y = [1/(b-a) for i in x]
plt.plot(x, y)
plt.xlabel('Value')
plt.ylabel('Probability')

# 누적분포함수 구현
y = [(i - a)/(b - a) for i in x]
plt.plot(x, y)
plt.xlabel('Value')
plt.ylabel('Probability')

확률밀도함수와 누적분포함수를 구현한 코드를 실행하면 아래와 같은 결과를 얻을 수 있다. 

그림3: 균등분포에서 확률밀도함수와 누적분포함수의 구현

정규 분포(Normal Distribution)

정규분포는 가장 일반적인 분포라고 알려져 있다. 그 이유는  중심극한정리(Central Limit Theorem)에 의해서 충분히 많은 독립적인 샘플들의 평균은 그 분포와 무관하게 정규분포에 수렴하기 때문이다. 정규분포의 형태는 평균과 분산으로 결정되며, 평균은 위치를 결정하고, 분산은 데이터의 퍼짐 정도를 결정한다. 정규분포는 아래 식으로 나타낸다. 

식3: 정규분포

정규분포는 연속형 확률변수, 대칭성, 벨 모양 곡선, 정규분포 그래프의 아래 부분의 합은 1이어야 한다는 성질을 가진다. 그리고 이 분포를 나타내기에 가장 적합한 것이 자연상수 e를 사용한 지수함수이다. 종모양으로 중심에 값이 몰리고 양쪽으로 값이 퍼지는 형태가 나오기 때문이다. 여기에 곡선 아래 면적을 정확히 1로 만들어주는 상수인 정규화 상수를 감안해 주면 아래와 같은 정규분포의 확률밀도 함수를(PDF) 구할 수 있다. 

식4: 정규분포의 확률밀도 함수(PDF)

x 축의 기준점을 잡아주고 위 식 4를 그대로 코드로 적으면 간단하게 시각화가 가능하다.

# 평균 0, 표준편차 1로 가정
mu_1 = 0
sigma_1 = 1
# x 값 -8 ~ 8 까지 200개의 균일한 변수 임의로 설정
x = np.linspace(-8, 8, 200)
# 정규분포 식에 대입
y_1 = (1/(np.sqrt(2 * np.pi * sigma_1**2))) * np.exp(-(x - mu_1)**2 / (2 * sigma_1**2))
# 시각화
plt.plot(x, y_1)
plt.xlabel('Value')
plt.ylabel('Probability')

그림4: 정규분포 시각화

정규분포에서는 표준편차 범위 안에 샘플이 포함될 확률이 아래와 같이 정의된다. 

식5: 정규분포의 성질

표준정규분포(Standard Normal Distribution)

정규분포화 된 변수의 비교 및 주어진 값에 대한 누적분포함수(CDF) 값을 쉽게 찾기 위해서 확률변수들을 표준정규분포로 변환하기도 한다. 확률변수를 표준화(Standardization) 하기 위해서 그 변수에서 평균을 빼고 표준편차로 나누는 과정을 거친다. 

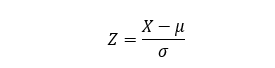
식6: 표준정규분포 변환 식

각각의 확률변수들을 표준화하는 과정을 거치면 평균이 0, 표준편차가 1인 표준정규분포로 바뀐다.