주요 함수와 함수의 변형

주요 함수의 종류

대수함수

아래 다항함수, 무리함수, 유리함수와 같이 다항식에 대수적인 연산(덧셈, 뺄셈, 곱셈, 나눗셈, 제곱근)을 적용해서 만든 것을 말한다.

다항함수

아래와 같은 식으로 표현되는 식을 다항함수라고 한다. 모든 다항식의 정의역은 실수(-무한대, +무한대)이다. 

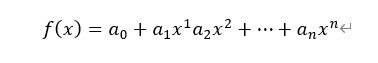
그림1: 다항함수

무리함수

a 가 상수일 때 아래와 같은 형식의 함수를 무리함수라고  한다.

그림2: 무리함수

유리함수

아래 식과 같이 두 다항식의 비로 나타나는 함수를 의미한다.

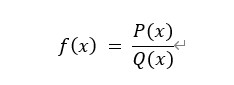
그림3: 유리함수

위에서 P(x), Q(x)는 각각 위에서 소개한 다항함수가 된다. 

초월함수

아래 삼각함수, 지수함수, 로그함수와 같이 대수적인 연산으로 표현할 수 없는 함수이다.

삼각함수

아래와 같이 sin, cos, tan 등으로 표시되는 함수이다. 

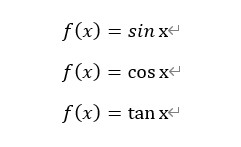
그림4: 삼각함수

미적분학에서는 관습적으로 라디안(호도) 단위로 x를 표현한다. 

지수함수

밑  a 가 양수일 때, 아래와 같은 형태를 가지는 함수이다.

그림5: 지수함수

로그함수

밑 a 가 양수일 때, 아래와 같은 형태를 가지는 함수이다. 

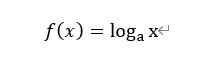
그림6: 로그함수

함수의 변형

수직과 수평이동

함수에 아래와 같이 상수(아래 예시에서는 상수 c )를 붙여서 좌우상하로 함수를 이동시키는 것을 말한다. 상수를 y 값에 붙이는지, x 값에 붙이는지 상수의 부호가 무엇인지에 따라 아래와 같이 함수를 이동시킬 수 있다.

그림7: 함수의 이동

압축 확장 대칭

아래 식처럼 함숫값 또는 변수(x)에 계수를 붙여서 함수의 형태를 늘리거나 압축하거나 대칭시키는 것을 말한다. 아래 예시에서 c > 1 이면 x 값에 따른 함수 f(x) 값이 c 만큼 더 배가 되므로 함수가 수직으로 늘어나게 된다.

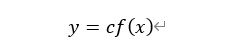
그림8: 함수의 압축확장 대칭 예시

함수의 결합

함수의 결합은 아래와 같이 함수끼리 사칙연산(덧셈, 뺄셈, 곱셈, 나눗셈)을 하는 것뿐만 아니라 함성함수를 만드는 것까지 포함한다. ( 아래 그림 9의 맨 아래쪽 식이 합성함수의 식이다. )

그림9: 함수의 결합

위 그림9의 마지막 식인 합성함수를 조금 더 설명하면, 아래 식 1에서 f(x)와 g(x)를 각각 정의하면, f(x) 의 x 에 g(x) 를 그대로 대입하면 그림 10과 같이 합성함수 f "써클" g를 표현할 수 있다.

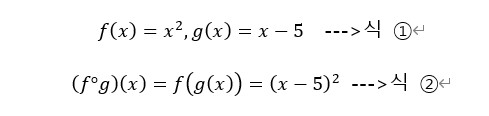
그림10: 합성함수