-
파이썬을 활용한 주가 경로 구하기: ELS Valuation2금융퀀트/자산평가&프로그램매매 2023. 12. 16. 10:41반응형
주가경로 산출 식
기하 브라운 운동을 따르는 주가의 움직임을 표준 정규분포로 모델링하면 아래와 같다. 아래 식을 이용해서 파이썬을 활용한 주가 변동성 구하기: ELS Valuation1에서 구한 S&P500 지수의 주가 변동성을 바탕으로 S&P500 지수의 주가 경로를 예측해 보자.

식1: 주가 경로의 기본 식 위 식에 따르면 다음 시간 단위의 주가는 현재주가, 무위험 수익률, 기초자산의 변동성, 랜덤워크를 따르는 임의의 수 인 z를 이용해서 구할 수 있다. 현재주가는 기준 시점의 주가일 것이고, 무위험 수익률은 기준 시점의 3 개월 CD금리 같은 시장에서 기초자산으로 인식되는 수익률이다. 그리고 z는 평균이 0, 분산이 1 인 표준정규분포에서 뽑아낸 임의의 난수이다.
파이썬을 이용한 주가경로 구하기
무위험 수익률 구하기
이번 작업에서 주가경로 산출의 기간은 2023-11-27~ 2026-12-04 로 할 것이다.(평가 대상이 될 ELS의 계약기간) 그리고 2023-11-27 시점의 S&P500 지수의 주가를 100으로 잡고 주가 경로를 구할 것이다. 왜냐하면 우리에게 중요한 것은 주가의 절대적인 수치가 아니라 S&P500 지수가 기준 시점을 기준으로 얼마나 움직이는지이기 때문이다. 무위험 수익률은 S&P500라는 USD 자산의 경로를 측정하는 것이기 때문에 USD 금리를 기준으로 해야 한다. USD 무위험 수익률은 현재 SOFR라는 금리로 뉴욕 연방준비위원회 홈페이지에서 아래와 같이 찾을 수 있다.

그림1: SOFR 금리(연방준비위원회 뉴욕 홈페이지) 위 그림 1에서 2023-11-27의 금리는 5.32% 이다.
변동성 구하기: Get_Variance 함수 만들기
기초자산의(S&P500 지수) 변동성을 구하는 방법은 파이썬을 활용한 주가 변동성 구하기: ELS Valuation1에서 자세하게 살펴봤다. 다시 한번 정리하면 먼저 가상환경을 만들고 필수 라이브러리를 설치한 뒤 (파이썬을 활용한 주가 변동성 구하기: ELS Valuation1 참조) yfinance의 download 메서드를 이용해서 S&P500 지수의 가격정보를 가져온다. 받아온 가격정보에 "Adj Close"라는 조정 종가 컬럼이 있는데 이 컬럼에 대해서 pct_change() 메서드를 이용해서 일일 수익률을 구한다.(지수의 수준에 영향을 받지 않고 상대적인 움직임을 측정해야 하기 때문에) 이렇게 구한 일일 수익률의 표준편차를 return 하면 된다. 코드로 정리하면 아래와 같다.
# 필요한 라이브러리들 pip install 을 통한 설치 import yfinance as yf import numpy as np import pandas_market_calendars as mcal from datetime import datetime import pandas as pd class SNP500ELS001(): # 클래스 인스턴스 설정 시 ticker와 calener 명을 넣어야 함 def __init__(self, ticker: str, calendar: str): self.ticker = ticker self.cal = calendar # Get_Variance 함수 설정 def Get_Variance(self, startdate: str, enddate: str): # 아래 시작일과 종료일 입력받아서 종가 데이터 입수 asset_price = yf.download(self.ticker, start=startdate, end=enddate) # 종가 데이터를 통한 일일 변화율 산출(dropna 로 null 값 제거) asset_returns = asset_price["Adj Close"].pct_change().dropna() # 변화율 데이터를 이용한 표준편차 계산 asset_vol = np.std(asset_returns) return asset_vol시간 단위 구하기: Get_TimeUnit 함수 만들기
무위험 수익률, 변동성, 기준주가(=100)까지 정했고 마지막으로 시간단위 "△t"를 구해야 한다. 이번 작업에서 주가경로 산출의 기간은 2023-11-27~ 2026-12-04로

식2: 시간 단위 식 그런데 2023-11-27 ~ 2026-12-04까지의 일 수에서 S&P500 지수가 나오지 않는 뉴욕증시가 쉬는 날은 빼야한다. 즉, 2023-11-27 ~ 2026-12-04 까지 뉴욕증시의 영업일의 개수가 분모가 된다. 뉴욕증시의 영업일 데이터를 받아오는 것이 문제인데 pandas_market_calendars 라이브러리의 get_calendar 메서드를 이용하면 된다. get_calendar 메서드의 변수로 뉴욕증시 달력을 나타내는 "XNYS"를 넣으면 뉴욕증시 영업일 인스턴스를 만들 수 있고, 해당 인스턴스에 valids_days라는 메서드를 사용하고 투입변수로 시작일과 종료일을 넣으면 영업일 목록을 받아올 수 있다.
주의할 부분은 get_calendar 메서드로 받아온 일자들은 전부 Timestamp라는 형식으로 시, 분, 초까지 표시된 시간 표시 형식이라는 점이다. 식 2에서 하루를 기준으로 시간 단위를 잡았는데 get_calendar에서 받아온 날짜들은 시, 분, 초까지 표시된 형식이므로 일관성이 맞지 않다. 따라서 영업일 데이터를 문자열 형식으로 저장했다가 다시 "YYYY-MM-DD"라는 일자까지만 표시된 날짜형식으로 바꾸는 과정이 필요하다. 이 내용을 코드로 정리하면 아래와 같다.
# 필요한 라이브러리 import yfinance as yf import numpy as np import pandas_market_calendars as mcal from datetime import datetime import pandas as pd class SNP500ELS001(): # 클래스 인스턴스 선언시 ticker 와 달력을 변수로 받음 이때 달력에 "XNYS"가 들어갈 것임 def __init__(self, ticker: str, calendar: str): self.ticker = ticker self.cal = calendar ...(생략)... def Get_TimeUnit(self, startdate: str, enddate: str): # calname 이라는 달력 인스턴스 생성 calname = mcal.get_calendar(self.cal) # 문자열로 받은 시작일을 날짜형식으로 type 변경 stdate = datetime.strptime(startdate, "%Y-%m-%d") # 문자열로 받은 종료일을 날짜형식으로 type 변경 eddate = datetime.strptime(enddate, "%Y-%m-%d") # 뉴욕 영업일 데이터에서 시작일~ 종료일 사이의 영업일 목록을 만들기 schedule = calname.valid_days(start_date=stdate, end_date=eddate) # 입수한 Timestamp 형식 영업일 데이터를 문자열형식으로 변환해서 list 데이터에 넣기 datestrlist = [date.strftime('%Y-%m-%d') for date in schedule] # 문자열형식 데이터를 다시 날짜형식으로 변환해서 리스트에 저장 datelist = [datetime.strptime(date, '%Y-%m-%d') for date in datestrlist] # 날짜 리스트 return return datelistreturn 된 datelist 의 개수를 len(datelist)로 구하고 이를 분모로 두면 ( = 1/ len(datelist) ) 시간 단위를 구할 수 있다.
현재 주가를 이용한 미래 주가 구하기: GeometricBrownianMotion 함수 만들기
현재주가, 변동성, 무위험 수익률, 시간 단위까지 전부 구할 수 있게 되었기 때문에 다음 기의 주가를 구할 수 있는 GeometricBrownianMotion을 나타내는 함수를 아래와 같이 코드로 정리할 수 있다. 평균이 0, 분산이 1 인 표준정규분포에서 뽑아낸 임의의 난수인 z는 numpy 라이브러리의 random.randn()이라는 메서드로 구할 수 있다.
import yfinance as yf import numpy as np import pandas_market_calendars as mcal from datetime import datetime import pandas as pd class SNP500ELS001(): def __init__(self, ticker: str, calendar: str): self.ticker = ticker self.cal = calendar ...(생략)... # curvalue: 현재주가, rfr: 무위험수익률, asset_vol: 자산변동성, timeunit: 시간단위 # 변수로 받는 함수 def GeometricBrownianMotion(self, currentvalue: float, rfr: float, asset_vol: float, timeunit: float): z = np.random.randn() delta_t = 1/timeunit # 위 식 1을 그대로 코드로 나타낸 부분 nextvalue = currentvalue * np.exp((rfr - 0.5*(asset_vol**2))*delta_t \ + asset_vol*np.sqrt(delta_t)*z) return nextvalue주가경로 구하기: Get_StochasticStockProcess 함수 만들기
Get_TimeUnit 함수에서 구한 datelist 즉, 영업일 list를 순차적으로 넣어서 GeometricBrownianMotion 함수에 넣어주면 다음 시간 단위의 주가를 순차적으로 구할 수 있다. 주가경로가 나오는 것이다. 결국, 주가경로 데이터는 "일자", "주가"로 이루어진 하나의 데이터프레임이 될 것이다.

그림2: 주가 시나리오 예시 그리고 주가 경로는 평균이 0, 분산이 1 인 표준정규분포에서 뽑아낸 임의의 난수인 z가 들어가기 때문에 반복할 때마다 다른 경로를 보여주게 된다. 이런 주가 경로를 무수히 많이 만들어내서 결과를 보는 것이 몬테카를로 시뮬레이션이다. 주가경로의 반복 횟수를 SENARIO1, SENARIO2, SENARIO3, ... 이런 식으로 이름을 붙인다면 아래 그림 3처럼 "DATE"컬럼을 기준으로 통합된 데이터를 붙여나갈 수 있다.

그림3: 일자별 주가시나리오 데이터 만들기 최종적으로 일자별로 시나리오마다 어떤 주가가 나오는지를 보여주는 하나의 데이터 프레임을 아래와 같이 만들 수 있다.
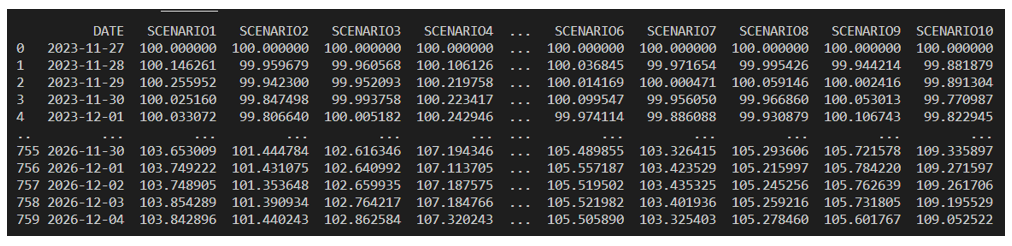
그림3: 일자별 주가경로 시나리오별 데이터 그림 3의 데이터 프레임을 만드는 과정을 나타내는 전체 코드는 아래와 같다.
import yfinance as yf import numpy as np import pandas_market_calendars as mcal from datetime import datetime import pandas as pd class SNP500ELS001(): def __init__(self, ticker: str, calendar: str): self.ticker = ticker self.cal = calendar def Get_Variance(self, startdate: str, enddate: str): asset_price = yf.download(self.ticker, start=startdate, end=enddate) asset_returns = asset_price["Adj Close"].pct_change().dropna() asset_vol = np.std(asset_returns) return asset_vol def Get_TimeUnit(self, startdate: str, enddate: str): calname = mcal.get_calendar(self.cal) stdate = datetime.strptime(startdate, "%Y-%m-%d") eddate = datetime.strptime(enddate, "%Y-%m-%d") schedule = calname.valid_days(start_date=stdate, end_date=eddate) datestrlist = [date.strftime('%Y-%m-%d') for date in schedule] datelist = [datetime.strptime(date, '%Y-%m-%d') for date in datestrlist] return datelist def GeometricBrownianMotion(self, curvalue: float, rfr: float, asset_vol: float, timeunit: float): z = np.random.randn() delta_t = 1/timeunit nextvalue = curvalue * np.exp((rfr - 0.5*(asset_vol**2))*delta_t \ + asset_vol*np.sqrt(delta_t)*z) return nextvalue # 주가경로를 최종적으로 만들어내는 함수 def Get_StochasticStockProcess(self, maxno: int, rfr: int, assetvol: int, timeunit: int, datelist): # 빈 데이터프레임 만들기: 단위 데이터 프레임을 합칠 전체 데이터 프레임 totdf = pd.DataFrame() # 변수로 받은 시뮬레이션횟수(maxno)만큼 시나리오 만들기 for simulationno in range(1, maxno+1): # 단위 데이터 프레임 컬럼 정의 "DATE", "SCENARIO&시도횟수" columns = ["DATE", f"SCENARIO{simulationno}"] # 단위 데이터 프레임 만들기 subdf = pd.DataFrame(columns=columns) # 결과를 list 에 담기위한 빈 list 생성 results = [] # 변수로 받은 datalist마다 for 문을 통해 작업 for date in datelist: # datelist[0] 즉, 첫째날짜일 경우 basevalue 처리(최초 시작점의 가치) if date == datelist[0]: curvalue = basevalue result = [date, curvalue] results.append(result) # datelist[0]보다 클 경우는 GeometricBrownianMotion 함수로 다음기의 주가 계산 else: nextvalue = self.GeometricBrownianMotion(curvalue, rfr, assetvol, timeunit) # 주가를 GeometricBrownianMotion 함수로 구한 value로 최신화 curvalue = nextvalue # 결과를 list화 하기 result = [date, curvalue] # 단위 결과 list를 모아서 시나리오 한 단위의 결과 list인 results만들어가기 results.append(result) # 시나리오 한 단위의 결과인 results를 subdf 로 데이터 프레임으로 만들기 subdf = pd.DataFrame(data=results, columns=columns) # 시나리오 한 단위의 결과인 단위 데이터프레임 subdf 를 # 기존까지 작업한 데이터인 totdf 와 mergre 로 합치기 if simulationno == 1: totdf = subdf else: totdf = pd.merge(totdf, subdf, on="DATE") return totdf if __name__ =="__main__": # SNP500ELS001 클래스에 "^GSPC"(ticker), "XNYS"(달력명)를 넣어서 els 인스턴스 만들기 els = SNP500ELS001("^GSPC", "XNYS") # 시뮬레이션 기간 만들기 contractdates = ["2023-11-27", "2026-12-04"] # 변동성을 구할 기간 정하기 datadates = ["2007-06-01", "2009-06-30"] # els 인스턴스의 Get_Variance 함수를 통해 시작일과 종료일 사이의 변동성 구하기 assetvol = els.Get_Variance(datadates[0], datadates[1]) # 시뮬레이션 수행할 datelist를 els 인스턴스의 Get_TimeUnit 함수를 통해서 구하기 datelist = els.Get_TimeUnit(contractdates[0], contractdates[1]) # datelist의 개수가 단위 시간의 분모가 됨 timeunit = len(datelist) # 2023-11-27 의 가치를 100이라고 기준점을 잡음(basevalue = 100) basevalue = 100 # SOFR 금리 5.32% 입력 rfr = 0.0532 # 10 회 시나리오 시도 trialno = 10 # els 인스턴스의 Get_StochasticStockProcess 로 주가경로 구하기 totdf = els.Get_StochasticStockProcess(trialno,rfr, assetvol, timeunit, datelist) print(totdf)반응형'금융퀀트 > 자산평가&프로그램매매' 카테고리의 다른 글
파이썬을 활용한 ELS 가치 평가하기: ELS Valuation3 (0) 2024.01.01 NPV 계산기 (0) 2023.12.24 파이썬을 활용한 주가 변동성 구하기: ELS Valuation1 (0) 2023.12.14 ELS 가치평가 하기: ELS는 진짜 위험할까? (0) 2023.12.12 듀레이션 계산기 (0) 2023.08.11