Bootstrapping 1: 무이표채 금리 만들기 실습

1. 금융에서 붓스트래핑

  Bootstrapping 이라는 용어는 통계학, 컴퓨터 등에서 다양하게 쓰인다. 물론 금융에서도 이 용어는 중요하게 쓰인다. 금융 쪽을 전공했거나 이쪽에 조금만 관심이 있어도 하나하나 신발끈을 묶는다는 의미의 "Bootsrapping"이라는 용어 자체는 많이 들어봤을 것이다. 그러나 정작 실제로 "Bootstrapping" 과정을 식으로 적어놓은 것은 익숙할지라도 실제 데이터로 어떻게 "Bootstrapping"을 하는지 보여주는 책은 많지가 않다. 우리는 이하에서 "Bootstrapping"과정을 통해서 무이표채 금리와 선도금리를 직접 만들어보면서 어렴풋이 알고 있었던 "Bootstrapping"이라는 용어를 확실하게 이해하려고 한다. 

2. 기초 데이터 설정: 무이표채 금리가 필요한 이유

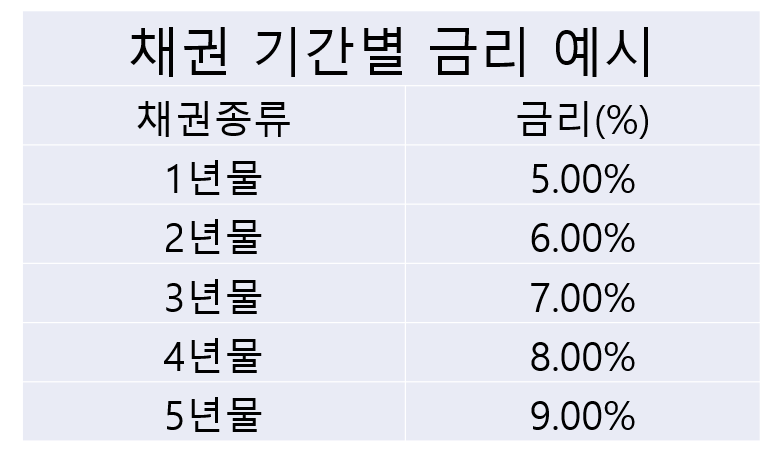
표1: 데이터 에시

  위 표처럼 시장에 채권이 5종류가 있다고 가정하자. 위 표에서 금리는 채권의 이표금리이고 1년마다 금리를 지급한다고 가정하자. 예를 들면, 위 표에서 3년 물 짜리 채권을 사서 만기까지 보유하면, 7%의 금리를 3번 받게 된다. 위의 금리를 가지고 우리는 금융자산의 NPV를 구할 수 있을까? 예를 들면, 3년짜리 금융자산의 현재가치를 구할 때, 위 표에서 3년 물의 금리가 7% 니까 아래와 같이 현재가치를 구하는 것이 정답일까? 

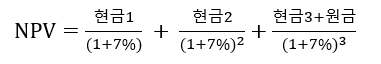
식1: NPV구하기

  정답이 아니다!! 이유는 위 표의 금리는 이표금리이기 때문이다. 즉 위 식 1에서 분자인 현금 부분을 결정해 주는 금리이기 때문이다. 다시 말하면 7%라는 금리는 아래 식과 같은 의미를 갖게 된다. 

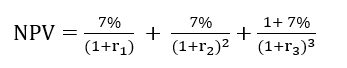
식2: NPV구하기2

그렇다면, 현재가치를 구할 때 사용하는 금리는 어떻게 구할 수 있을까? 위 식 2에서 분모 r 들은 어떻게 구할 수 있을까? 이를 구하는 과정이 무이표채 금리 커브 Bootstrapping이다. 

3. Bootstrapping : 무이표채 금리 커브 만들기

  위 표 1의 상황에서 무이표채 금리의 의미는 "마지막에 한 방에 받는 수익률이 몇 % 이여야 위 표1처럼 금리가 1년 마다 지급되는 채권과 같은 수익을 낼 수 있는가?" 이다. 이 말을 위 표1의 1년 물 채권을 이용해서 나타내면 아래 식의 ①과 같이 되고 이를 정리하면 5% 라는 무이표금리를 구할 수 있다. 

식3: 무이표채금리 구하기1

2년 무이표 금리는 6%의 2년 물 채권을 통해서 아래와 같이 구할 수 있다. 

식4: 무이표채금리 구하기 2

3년 무이표금리는 위 방식과 마찬가지로 7%의 3년 물 채권을 통해서 아래와 같이 구할 수 있다. 

식5: 무이표채금리 구하기 3

같은 방식으로 5년 물까지 한 개씩 무이표금리를 구해나갈 수 있고 그 결과는 아래와 같은 표가 된다. ( 4년, 5년 무이표금리는 각자 구해보도록 하자! ) 

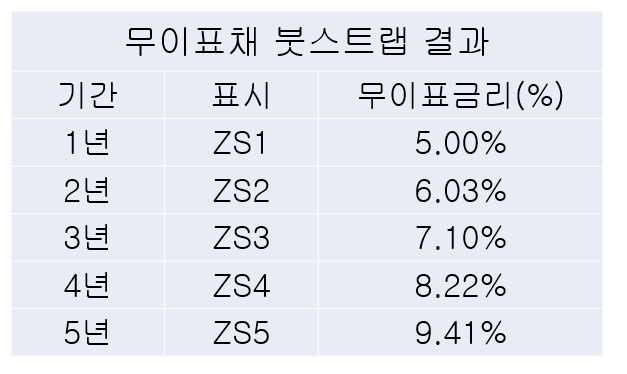
표2: Bootstrapping 결과

이렇게 주어진 이표금리 데이터를 가지고 1년 할인 금리를 구하고, 이를 다시 이용해서 2년 할인 금리를 구하고를 계속 반복하는 것이 바로 Bootstrapping이다.